Nếu bạn hay nhầm lần hoặc chưa biết cách vận dụng các công thức diện tích tam giác vào giải các bài tập toán liên quan thì cùng dientichtamgiac điểm lại các công thức và bài tập thường gặp qua bài viết sau đây. Chúng ta cùng nhau vào bài học nào.
1. Công thức tính diện tích tam giác thường
1.1 Công thức chung
${S_{ABC}} = \frac{1}{2}a.{h_a}$ $ = \frac{1}{2}b.{h_b}$ $ = \frac{1}{2}c.{h_c}$
Ví dụ: (Trích câu 1 trang 96 SGK Toán 5 KNTT tập 1)
Tính diện tích của hình tam giác, biết:
a) Độ dài đáy là 4 cm và chiều cao là 3 cm.
b) Độ dài đáy là 5 dm và chiều cao là 8 dm.
Lời giải
a) Theo đề ta có:
- BC = 4 cm
- AH = h = 3 cm
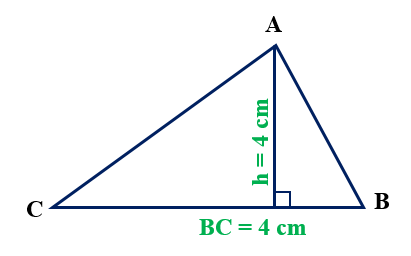
Diện tích hình tam giác là: $\frac{{4 \times 3}}{2} = 6$ (cm2)
b) Theo đề ta có:
- BC = 5 dm
- AH = h = 8 dm
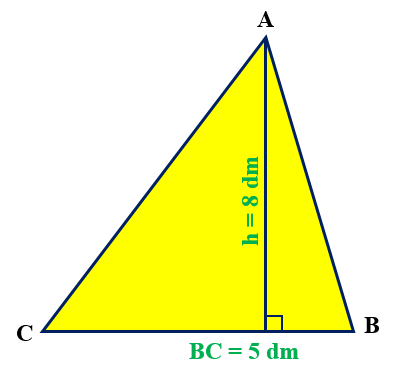
Diện tích hình tam giác là: $\frac{{5 \times 8}}{2} = 20$ (dm2)
1.2 Tính diện tích tam giác khi biết một góc
${S_{ABC}} = \frac{1}{2}a.b.\sin \widehat C$ $ = \frac{1}{2}a.c.\sin \widehat B$ $ = \frac{1}{2}b.c.\sin \widehat A$
Ví dụ: Cho tam giác ΔABC, biết AC = 4 cm; BC = 5 cm và góc tạo bởi AC với BC là 300.
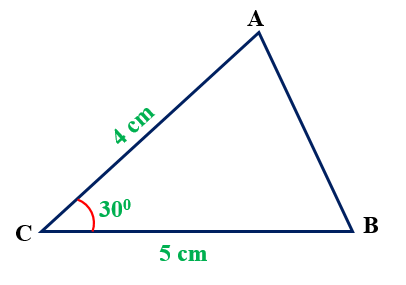
Hãy tính diện tích tam giác ΔABC.
Lời giải
Ta có:
- AC = 4 cm;
- BC = 5 cm
- $\widehat C$ = 300
Diện tích tam giác: ${S_{\Delta ABC}} = \frac{1}{2}AC.CB.\sin \widehat C$ $ = \frac{1}{2}.4.5.\sin {30^0}$ $ = 5\left( {c{m^2}} \right)$
1.3. Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
${S_{\Delta ABC}} = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} $
Với $p = \frac{1}{2}\left( {a + b + c} \right)$
Ví dụ: Cho tam giác ΔABC, biết AB = 4 cm; BC = 5 cm và CA = 6 cm.
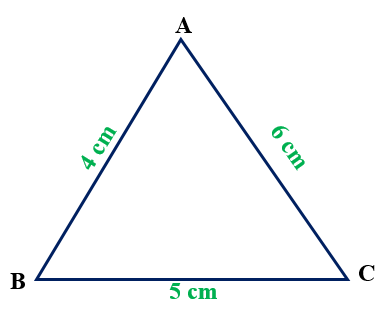
Hãy tính diện tích tam giác ΔABC.
Lời giải
Theo đề bài:
- AB = 4 cm;
- BC = 5 cm;
- CA = 6 cm;
Ta có: $p = \frac{1}{2}\left( {a + b + c} \right)$ $ = \frac{1}{2}\left( {4 + 5 + 6} \right)$ $ = 7,5\left( {cm} \right)$
Áp dụng công thức Heron, ta có diện tích tam giác:
${S_{\Delta ABC}} = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} $
$ = \sqrt {7,5.\left( {7,5 – 5} \right)\left( {7,5 – 6} \right)\left( {7,5 – 4} \right)} $
$ = \frac{{15\sqrt 7 }}{4}$
1.4. Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).
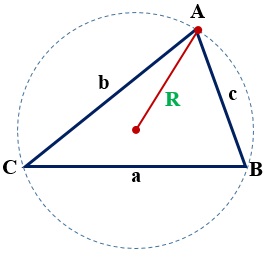
${S_{ABC}} = \frac{{abc}}{{4R}}$
hoặc ${S_{ABC}} = 2.{R^2}.\sin \widehat A.\sin \widehat B.\sin \widehat C$
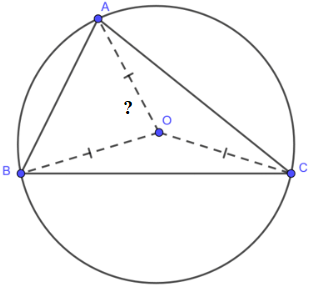
Ví dụ 1. Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.
Lời giải
Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
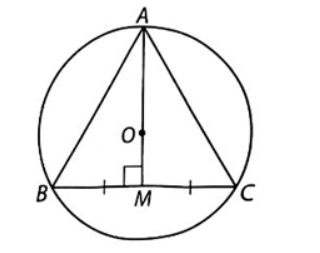
Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao, đường trung tuyến trong tam giác đều ABC.
Do đó: \(OA = \frac{{BC\sqrt 3 }}{3} \Rightarrow BC = \sqrt 3 OA = 3\sqrt 3 \left( {cm} \right)\)
Vì O là trọng tâm của tam giác ABC, AH là đường trung tuyến của tam giác ABC nên \(AH = \frac{3}{2}OA = \frac{3}{2}.3 = \frac{9}{2}\left( {cm} \right)\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}AH.BC = \frac{1}{2}.\frac{9}{2}.3\sqrt 3 = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ví dụ 2. Tính chu vi và diện tích của tam giác đều nội tiếp một đường tròn bán kính 3cm.
Lời giải
Gọi h(cm), a(cm) lần lượt là chiều cao, cạnh của tam giác đều.
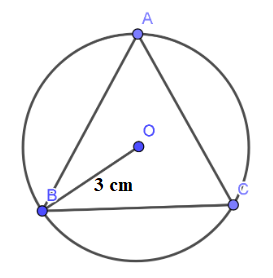
Suy ra: \(\frac{2}{3}h = 3\). Do đó, \(h = 4,5cm\)
Lại có: \(\frac{{\sqrt 3 }}{3}a = 3\) nên \(a = 3\sqrt 3 \left( {cm} \right)\).
Chu vi của tam giác là: \(C = 3a = 9\sqrt 3 \left( {cm} \right)\).
Diện tích của tam giác là: \(S = \frac{1}{2}a.h = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\).
Ví dụ 3. Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải
Theo công thức Hê – rông, diện tích tam giác ABC:
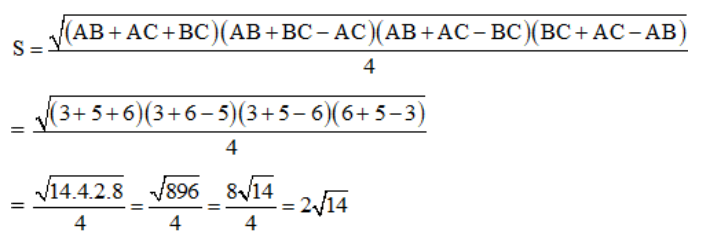
Khi đó, bán kính của đường tròn ngoại tiếp tam giác ABC là:
$R = \frac{{AB.AC.BC}}{{4S}}$ $ = \frac{{3.5.6}}{{4.2\sqrt {14} }}$ $ = \frac{{90}}{{8\sqrt {14} }}$ $ = \frac{{45}}{{4\sqrt {14} }}$
1.5. Tính diện tích tam giác bằng bán kính đường tròn nội tiếp tam giác (r).
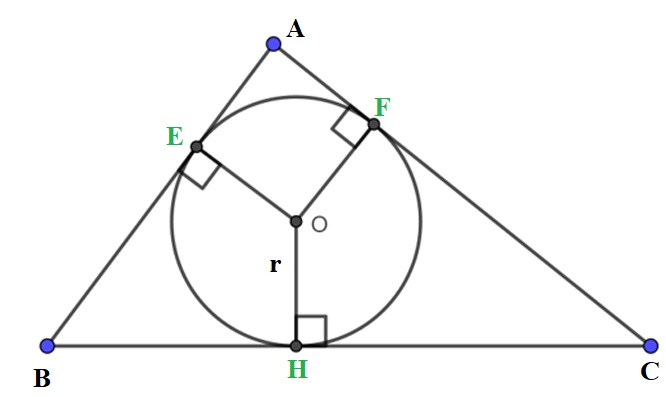
SΔABC = p.r
- p: Nửa chu vi tam giác.
- r: Bán kính đường tròn nội tiếp.
Ví dụ 1: Tính chu vi và diện tích của tam giác đều ngoại tiếp một đường tròn bán kính 3cm.
Lời giải
Gọi h(cm), a(cm) lần lượt là chiều cao, cạnh của tam giác đều.
Suy ra: \(\frac{1}{3}h = 3\). Do đó, \(h = 9cm\)
Lại có: \(\frac{{\sqrt 3 }}{6}a = 3\) nên \(a = 6\sqrt 3 \left( {cm} \right)\).
Chu vi của tam giác là: \(C = 3a = 18\sqrt 3 \left( {cm} \right)\).
Diện tích của tam giác là: \(S = \frac{1}{2}a.h = 27\sqrt 3 \left( {c{m^2}} \right)\).
Ví dụ 2. Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm.
Lời giải
Ta có bán kính đường tròn nội tiếp tam giác đều là r = \(\frac{{a\sqrt 3 }}{6}\).
(Với a là độ dài cạnh của tam giác đều)
Mà r = 1 cm suy ra \(\frac{{a\sqrt 3 }}{6} = 1\) hay a = \(\frac{6}{{\sqrt 3 }} = 2\sqrt 3 \) (cm).
Vì tâm của đường tròn nội tiếp tam giác đều là giao điểm của ba đường phân giác nên cũng chính là trọng tâm của tam giác đều nên đường cao của tam giác đều đồng thời là đường trung tuyến của tam giác đều là:
\(h = 3.r = 3.1 = 3\) (cm)
Diện tích tam giác đều là:
\(S = \frac{1}{2}.a.h = \frac{{1}}{2}.2\sqrt 3 .3 = 3\sqrt 3 \) (cm2).
2. Diện tích tam giác vuông
Tam giác ABC vuông tại B, a, b là độ dài hai cạnh góc vuông. Khi đó ta áp dụng công thức tính diện tích phần chung ta suy ra được:
${S_{ABC}} = \frac{1}{2}a.b$
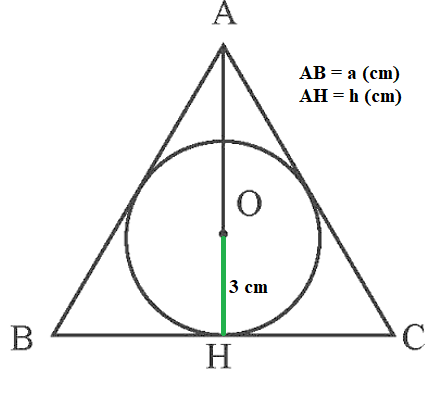
3. Diện tích tam giác cân
Tam giác cân ABC có ba cạnh, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, ha là đường cao từ đỉnh A như hình vẽ. Áp dụng công thức tính diện tích chung, ta có công thức tính diện tích tam giác cân:
${S_{ABC}} = \frac{1}{2}a.{h_a}$
4. Diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông. Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:
${S_{ABC}} = \frac{1}{2}{a^2}$
5. Diện tích tam giác đều
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh như hình vẽ. Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích tam giác đều:
${S_{ABC}} = \frac{1}{2}{a^2}.\frac{{\sqrt 3 }}{4}$